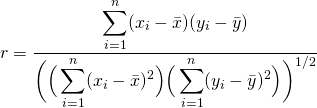JavaScriptでユークリッド距離とピアソン相関係数

2016.05.03

この記事は最終更新日から1年以上が経過しています。

今回は、口コミサイトなどによくあるユーザーレビューの評価から、似ているユーザーを探すアルゴリズムについて少々書いていきます。

例えば、ゲームのレビューデータがこの様な感じで存在したとします。

タイトル \ ユーザー	takayama	nakamura	tanaka	koike
ドラゴンクエスト	10	7	8	3
スーパーマリオ	9	5	10	8
ゼルダの伝説	4	8	5	10
F-ZERO	7	7	8	6
ファイナルファンタジー	5	6	8	10

これらのデータを元に、似ているユーザーを探し出します。

それぞれのユーザーをすべてのユーザーと比較し、どの程度似ているか類似性スコアと言われるものを算出して比較していきます。

類似性スコアの算出方法は幾つもありますが、もっとも初歩的な「ユークリッド距離」と「ピアソン相関係数」によって算出していきたいと思います。

ユークリッド距離

類似性スコアの算出方法で単純な方法の一つで、「ユークリッド距離」と呼ばれるものがあります。

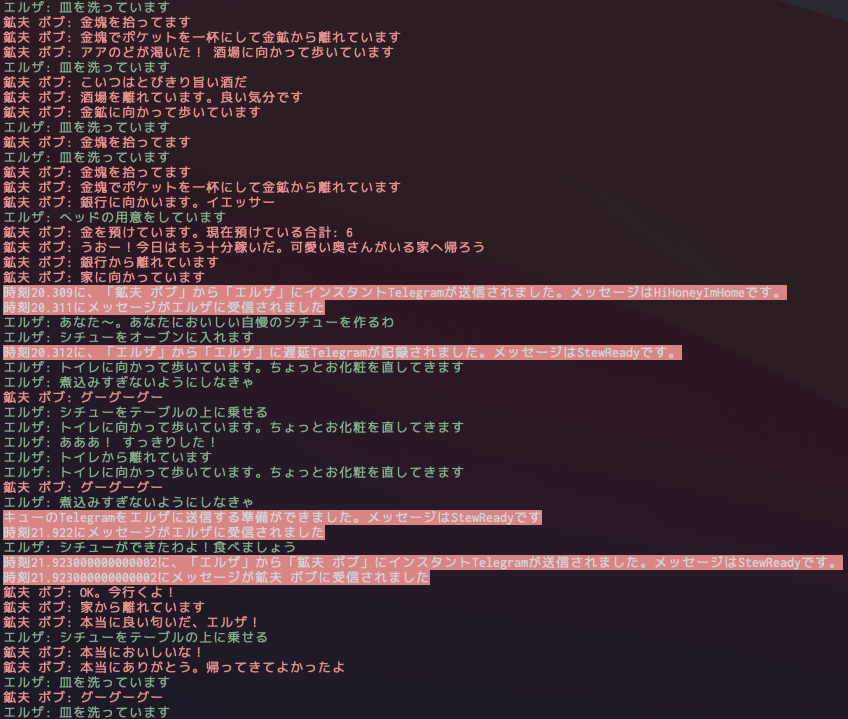
端的に説明させていただきますと、ユーザーが評価したアイテムを軸にしグラフを表示します。

グラフ上にユーザーを配置し、各ユーザーの距離を算出する事によってどのくらいユーザー同士は近いかを計算する方法となります。

まず、例に上記の表から「ドラゴンクエスト」と「スーパーマリオ」を比較して、ユーザーを嗜好空間に図示してみます。

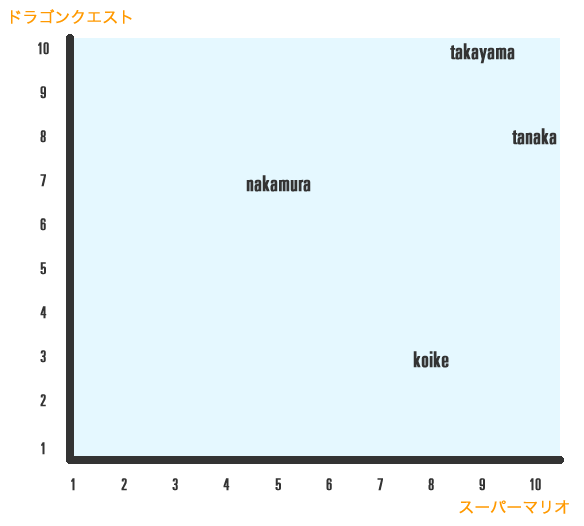
パッと見た感じ「takayama」と「tanaka」は近く、「takayama」と「koike」は遠いのが分かるかと思います。

では、これをユークリッド距離と言われる計算式によって算出してみましょう。

ユークリッド距離の定義

$$$ d(p,q)=d(q,p)=\sqrt{(q_1-p_1)^2+(q_2-p_2)^2+\cdots+(q_n+p_n)^2} \\$

比較的シンプルな計算式によって答えを導く事が出来ます。

上記の定義式より更に1を加えることによって、0から1を返す式にします。

こうすることによって、より類似性の高いユーザーは1に近くなり、類似性の低いユーザーは0に近くなります。

「takayama」と「tanaka」の「ドラゴンクエスト」と「スーパーマリオ」におけるユークリッド距離。

var distance = 1/(1 + Math.sqrt(Math.pow(10-8,2) + Math.pow(9-10,2)));

result

0.3090169943749474

「takayama」と「koike」の「ドラゴンクエスト」と「スーパーマリオ」におけるユークリッド距離。

var distance = 1/(1 + Math.sqrt(Math.pow(10-3,2) + Math.pow(9-8,2)));

result

0.12389934309929541

もちろんですが、全く同じにすると、1が返却されます。

var distance = 1/(1 + Math.sqrt(Math.pow(10-10,2) + Math.pow(4-4,2)));

result

このユークリッド距離をまとめて計算するJavaScriptの関数は以下の様になります。

function sim_distance(prefs, person1, person2) {
  var sumOfSquares = 0, matchItem = [];

  for(item in prefs[person1]) {
    if(item in prefs[person2]) {
      matchItem.push(item);
    }
  }

  // マッチするアイテムがない場合は処理しない。
  if(matchItem.length == 0) return;

  matchItem.forEach(function(val) {
    sumOfSquares += Math.sqrt(Math.pow(prefs[person1][val] - prefs[person2][val],2));
  });

  return 1 / (1 + sumOfSquares);
}

アイテムとユークリッド距離を算出したいユーザーを引数にする事によって、値を求めることができます。

sim_distance(reviews, "takayama", "tanaka");

このままでも良いのですが、より正確に類似性を高める為に洗練された方法としてピアソンの相関係数を求める方法があります。

相関係数とは2つのデータセットがある直線に沿ってどの程度沿っているかを示す数値となります。

上記では、点数が近いユーザーを類似性の高いユーザーとしてきましたが、果てしてそれで良かったでしょうか。

例えば、一方は点数を甘く付ける傾向があり、一方は全体的に厳しく点数を厳しく付ける傾向があるとき、

ユーザー間で点数差は開いているが、各評価の付け方の傾向が似ていた場合、それを類似性を高いとするか低いとするか。

アプリケーションによってその判定は異なるかと思いますが、その様な点数の付け方でも、嗜好の近いユーザーとして算出するのにピアソンの相関係数が使われたりします。

回帰直線と相関係数

先ほどの表のユーザー「takayama」と「tanaka」とを比較し、アイテムを配置した散布図を作成してみます。

散布図

b 2

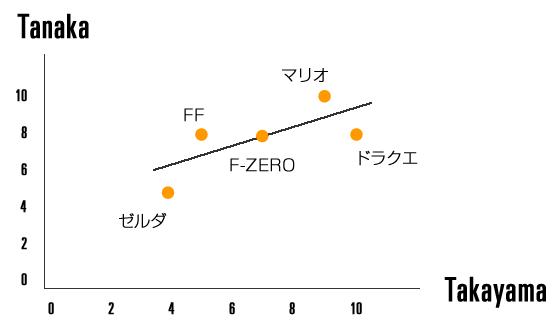
すべてのアイテムにできるだけ近く、右上に引かれている線が回帰直線と呼ばれるもので、

二人が全く同じ評点とする場合、直線上にすべてのアイテムが乗る形となります。

評価点が完全に相関していることになりますので、そのときのスコアは1となり、

ユーザー間の相関関係は強い事が示されます。

相関係数の絶対値	解釈
0.0〜0.2	ほとんど相関関係がない
0.2〜0.4	やや相関関係がある
0.4〜0.7	かなり相関関係がある
0.7〜1.0	強い相関関係がある

それでは、相関係数についてちょっとwikipediaを参照してみましょう。

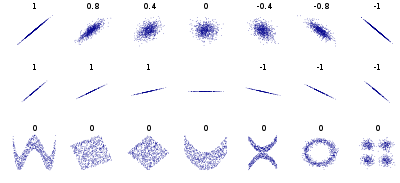
相関係数（そうかんけいすう、英: correlation coefficient）は、2つの確率変数の間にある線形な関係の強弱を測る指標である。相関係数は無次元量で、−1以上1以下の実数に値をとる。相関係数が正のとき確率変数には正の相関が、負のとき確率変数には負の相関があるという。また相関係数が0のとき確率変数は無相関であるという。

たとえば、先進諸国の失業率と実質経済成長率は強い負の相関関係にあり、相関係数を求めれば比較的−1に近い数字になる。

引用元：wikipedia

wikipedia 相関係数

ふむふむ。

正の相関と負の相関があるのがわかりますね。

負の相関の場合は、類似性の低い（異なる）ユーザーというのがわかりますね。

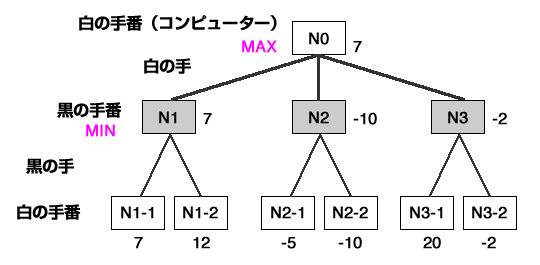
ピアソンの積率相関係数

相関係数について調べて見ると、

正の分散を持つ確率変数 $X$ 、 $Y$ が与えられたとき、共分散を $σ XY$ 、標準偏差を $σ X$ 、 $σ Y$ とおく。このとき

$$$ p = \frac{ \displaystyle \sigma{XY} }{ \sigma{X}\sigma{Y}}$

を確率変数 $X$ 、 $Y$ の相関係数という。これは期待値を $E [-]$ で表せば

$$$ p = \frac{ \displaystyle E\Big[(X - E[X])(Y - E[Y])\Big] }{ \bigg(E\Big[(X - E[X])^2\Big]E\Big[(Y - E[Y])^2\Big]\bigg)^{1/2} }$

と書き直すこともできる。

引用元：wikipedia

wikipedia 相関係数

うん。
書き直すことによって更にわかんなくなった気がしますね。w

更に、ピアソンの積率相関係数（Pearson product-moment correlation coefficient）について調べて見ると、

2組の数値からなるデータ列 $\{(x_{i}, \, y_{i})\} (i=1,2,\ldots,n)$ が与えられたとき、標本共分散をsxy、標本標準偏差をsx、syとおく。このとき
$r = \frac{s_{x y}}{s_x s_y}$
を標本相関係数（sample correlation coefficient）あるいはピアソンの積率相関係数という。これはデータ $x = \{x_{i}\}, y = \{y_{i}\}$ の相加平均を $\bar{x}、\bar{y}$ で表せば

$$$ r = \frac{ \displaystyle \sum_{i=1}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y}) }{ \bigg(\Big( \displaystyle \sum_{i=1}^n(x_{i}-\bar{x})^2 \Big)\Big( \sum_{i=1}^n(y_{i}-\bar{y})^2 \Big)\bigg)^{1/2} }$

と書き直すこともできる。
これは、幾何学的には各データの平均からのずれを表すベクトル
$$$ x-\bar{x} = (x_1-\bar{x},\ldots,x_n-\bar{x}), y-\bar{y} = (y_1-\bar{y},\ldots,y_n-\bar{y})$
のなす角の余弦である。

引用元：wikipedia

wikipedia 相関係数

と、wikipediaには記されておりますが、いやぁ、もう何が何だかですね。

いきなり難しくなった感じがありますよね。

でも、大丈夫です。一つ一つ噛み砕いていくと答えは見えてきます。

まず、定義されている式から見ていきましょう。

ピアソンの積率相関係数

$$$ r = \frac{ \displaystyle \frac{1}{N}\sum_{i=1}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y}) } { \displaystyle \sqrt{\frac{1}{N}\sum_{i=1}^n(x_{i}-\bar{x})^2} \sqrt{\frac{1}{N}\sum_{i=1}^n(y_{i}-\bar{y})^2} }$

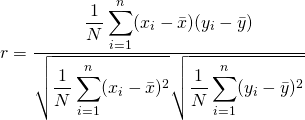
と、若干わかりやすくした式。

日本語で表すと、

スクリーンショット 2016-05-03 2.34.25

日本語に戻すと大分わかりやすい感じになりましたね。

更に、数式を演算子に起こしますと、

相関係数＝共分散 ÷ （ xの標準偏差 × yの標準偏差）

となります。

かなり理解しやすいですね。

そう、ピアソンの積率相関係数 r は，「変数 X と変数 Y の共分散」と「それぞれの変数の標準偏差」から求められるのです。

ですが、若干聞きなれない言葉「共分散」と「標準偏差」が出てきました。

それでは、それぞれ見ていきましょう。

標準偏差の計算

再びこちらの表を

タイトル \ ユーザー	takayama (x)	tanaka (y)
ドラゴンクエスト	10	8
スーパーマリオ	9	10
ゼルダの伝説	4	5
F-ZERO	7	8
ファイナルファンタジー	5	8

今回は、takayamaをx とし、tanakaをy として2人の相関係数を導いていきます。

求める値	計算式
平均	xの合計値 ÷ ゲーム（レビュー）数
偏差	ゲーム毎の値 – 平均
分散	偏差の二乗の合計÷ ゲーム（レビュー）数
標準偏差	分散の平方根（ルート）

平均

takayamaの各レビューの点数の平均を求めます。

(10 + 9 + 4 + 7 + 5) ÷ 5 = 7

平均点数は「7」となります。

偏差

先ほど求めた平均「7」を各点数から差し引いていきます。

その値が、各レビュー点数の偏差となります。

各レビュー点数 - 平均点 = 偏差

各ゲーム	偏差式	偏差
ドラゴンクエスト	10 – 7	3
スーパーマリオ	9 – 7	2
ゼルダの伝説	4 – 7	-3
F-ZERO	7 – 7	0
ファイナルファンタジー	5 – 7	-2

分散

分散は、データの「ばらつき」を表す値となっていて、偏差を二乗した平均を計算する事によって求められます。

偏差の二乗の合計 ÷ アイテム数 = 分散

各ゲーム	偏差の二乗
ドラゴンクエスト	3² = 9
スーパーマリオ	2² = 4
ゼルダの伝説	-3² = 9
F-ZERO	0² = 0
ファイナルファンタジー	-2² = 4

26 ÷ 5 = 5.2

ということで、takayama（x）の分散は「5.2」ということが求められました。

標準偏差

「標準偏差」の計算は、分散の平方根(ルート)を計算するだけで求められます。

標準偏差 = √分散

標準偏差: 2.280 = √5.2

ということで、takayama（x）の標準偏差は2.280と求められました。

同じく、tanaka（y）を計算すると標準偏差は1.600と求められました。

ではそれぞれ、表にまとめてみます。

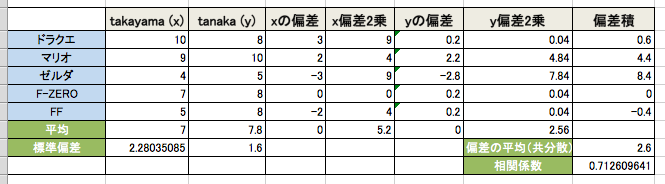
タイトル \ ユーザー	takayama (x)	x 偏差	x偏差2乗	tanaka (y)	y 偏差	y偏差2乗
ドラゴンクエスト	10	3	9	8	0.2	0.04
スーパーマリオ	9	2	4	10	2.2	4.84
ゼルダの伝説	4	-3	9	5	-2.8	7.84
F-ZERO	7	0	0	8	0.2	0.04
ファイナルファンタジー	5	-2	4	8	0.2	0.04
合計	35	0	26	39	0	12.8

分散：x 5.2, y 2.56

標準偏差：x 2.280, y 1.6

となりました。

あと、もう少しですね。

共分散

それでは、こちらの式の

スクリーンショット 2016-05-03 2.34.25

または、

相関係数＝共分散 ÷ （ xの標準偏差 × yの標準偏差）

共分散を求めれば、相関係数が出てきますね。

「共分散」は、ゲーム（アイテム）ごとの x と yの偏差（点数 – 平均）を掛け合わせた平均となります。

タイトル \ ユーザー	takayama(x) 偏差		tanaka (y)の偏差
ドラゴンクエスト	(10 – 7)	×	(8 – 7.8)	0.6
スーパーマリオ	(9 – 7)	×	(10 – 7.8)	4.4
ゼルダの伝説	(4 – 7)	×	(5 – 7.8)	8.4
F-ZERO	(7 – 7)	×	(8 – 7.8)	0
ファイナルファンタジー	(5 – 7)	×	(8 – 7.8)	-0.4

平均共分散：2.6

相関係数

それぞれ必要な情報は集まったので、相関係数の計算を行います。

スクリーンショット 2016-05-03 2.34.25

相関係数＝共分散 ÷ （ xの標準偏差 × yの標準偏差）

でしたので、 r = 共分散：2.6 /（takayama(x) 標準偏差 2.280 × tanaka（y）標準偏差 1.600)

となりますね。

r = 2.6 / （2.280 × 1.600)

係数 0.712609

と出ました！

こういうのもエクセルでやると早いですね。

スクリーンショット 2016-05-03 21.35.07

ちなみに回帰直線を含んだ分布図もサクッと作れます。

では、これらをJavaScriptで求めてみましょう。

function sim_pearson(prefs, person1, person2) {
  var matchItem = [];

  for(item in prefs[person1]) {
    if(item in prefs[person2]) {
      matchItem.push(item);
    }
  }

  // マッチするアイテムがない場合は処理しない。
  if(matchItem.length == 0) return;

  var sum1 = 0, sum2 = 0,
      sum1Sq = 0, sum2Sq = 0,
      pSum = 0, n = matchItem.length, r = 0;

  matchItem.forEach(function(val) {
    // 評価点の合計
    sum1 += prefs[person1][val];
    sum2 += prefs[person2][val];

    // 平方を合計する
    sum1Sq += Math.pow(prefs[person1][val], 2);
    sum2Sq += Math.pow(prefs[person2][val], 2);

    // 積を合計する
    pSum += prefs[person1][val] * prefs[person2][val];
  });

  var num = pSum - (sum1 * sum2 / n),
      den = Math.sqrt((sum1Sq - Math.pow(sum1, 2) / n) * (sum2Sq - Math.pow(sum2, 2) / n));

  if(den == 0) return;

  r = num / den;
  return r;
}

このように、アイテムと相関係数を算出したユーザーを引数にする事によって、相関係数が返ってきます。

sim_pearson(reviews, "takayama", "tanaka");

と、実行すると、上記で求めた係数と同様の数値が返って来るのが確認できます。

result

0.712609

今回は類似性スコアの算出方法として、初歩的な「ユークリッド距離」と「ピアソンの積率相関係数」その他にもあるので、興味のある方は調べてみるのも良いかも知れませんね。

このようにユーザー間の相関係数を求めることによって、レコメンドのアルゴリズなども作成することができますね。
いつかその辺も。。

ではではぁ。

このサイトは、只今WEB業界で活躍中のデザイナー、プログラマーの方々の情報を集めたweb統合情報サイトです。

web帳

Archives Details