5分で学ぶ RustでWave Function Collapse (波動関数崩壊アルゴリズム)
2024.01.15
この記事は最終更新日から1年以上が経過しています。

この記事は、5分で覚える Flutter Flameで作る Wave Function Collapse – 波動関数崩壊アルゴリズム
のRust版、5分で学ぶ RustとWave Function Collapse (波動関数崩壊アルゴリズム)の旅の、Rust実装箇所の抜粋記事となります。
WFCをRustで実装
それでは、仕様も出揃ったところなので実装に入って行きたいと思います。
今回は、言語にはRust、描画にはSDLを用いて実装を行います。
環境
- macOS Sonoma 14.1.1
- rustc 1.73.0
crates
- sdl2 0.36.0
- tokio 1
- serde 1.0
- serde_json 1.0
- num 0.4.1
- rand 0.8.5
WFCの大きな流れとしては、以下の初期設定を行います。
- タイルの画像、制約情報を入力データとする
- グリッド内にセルとして全ての可能性として保持
WFC実行フローとして、
- エントロピーの低いセルを優先するため、グループ化して取得
- タイルをランダムに選択、セルを1つの選択肢に確定。
- 隣接するセルのソケットを評価し、各セルのエントロピーを減少
- 伝播し終わると再度処理を実行
となり、全てのセルが崩壊、つまり1つの選択肢に確定となるとWFCの処理は終了となります。
タイルの画像、制約情報を入力データとする
まず、タイルの画像と制約情報を持ったデータの作成を行います。
JSONフォーマットで、用意します。スキーマの詳細は以下の通り。
- src: 画像のパス
- edges: 各エッジのソケット条件
- isRotate: 回転可能か否か
"tileList": [
{
"src": "simple/blank.png",
"edges": ["AAA", "AAA", "AAA", "AAA"],
"isRotate": false
},
{
"src": "simple/t.png",
"edges": ["AAA", "ABA", "ABA", "ABA"],
"isRotate": true
}]
}
edgesは、上、右、下、左の順番で記述しています。
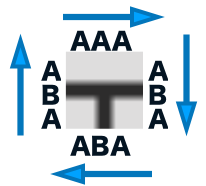
上部の端は、「左、中、右」、右部の端は、「上、中、下」、下部の端は、「右、中、左」、左部の端は、「下、中、上」といった順番で形でedgesに配列で記述していきます。
isRotateに関しては、「回転して利用できるか否か」になります。
単色のblankは回転して利用しても向き、形が何も変わりませんので回転する必要がなく、逆にT画像に関しては全ての向きの画像分の種類の用意の必要がなく、1つを時計回りに90度ずつ3回回転させて流用することで、1枚の画像で4パターン生成することが可能です。
なので、以下のパターンを網羅するには、2枚の画像があればカバーできますので2枚の画像で回転を含めた5パターンのタイルマップを用意することになります。

Grid、Tile classの作成
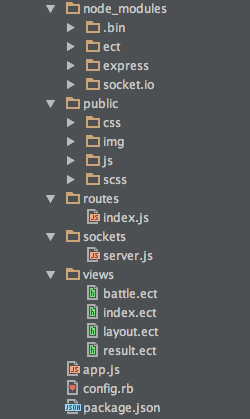
今回のディレクトリ構造は以下の様にしました。
ファイル構成
src/ ├── constants │ └── defines.rs ├── constants.rs ├── core │ ├── cell.rs │ ├── tile.rs │ └── wfc.rs ├── core.rs ├── main.rs ├── utility │ ├── error.rs │ └── utility.rs └── utility.rs
各ディレクトリの概要は、
- constants: 定数、コンフィグなど定義ファイル
- core: cell、tilesのstruct、WFCメインの処理
- utility: その他の処理
となっております。
それでは、実ソースの方を見ていきます。
まず、今回はSDLを用いているのもあり、main関数でsdl2の初期化を行い、(sdl2の初期化は割愛させていただきます) Cellのベクターを保持するgridと、Tileベクターを保持するtilesを用意します。
gridはタイルマップ全体となっており、タイルのマス分Cellが格納されます。
また、tilesは先程JSONファイルで用意したデータを元に生成されたTile classを格納することになります。
async fn main() -> Result<(), MyError> {
let sdl_context = sdl2::init()?;
let mut canvas = sdl_init(&sdl_context)?;
let texture_creator = canvas.texture_creator();
let tiles = init_tiles(&texture_creator).await?;
let mut grid: Vec<Cell> = init_grid(tiles.len());
...
Tile structは以下の様になります。
JSONファイルで定義したedges、isRotateを保持し、imageのpathを元にtextureを生成します。また、回転が必要であればangleの値も計算。
その他に、コネクトできるTileのindexを保持する配列、 up、right、down、leftを intのListで用意します。
pub struct Tile<'a> {
pub texture: Rc<Texture<'a>>,
pub edges: Vec<String>,
pub angle: f64,
pub is_rotate: bool,
pub up: Vec<usize>,
pub right: Vec<usize>,
pub down: Vec<usize>,
pub left: Vec<usize>,
}
init_tiles関数で、canvas.texture_creatorを引数に、JSONデータよりTileのインスタンスを生成します。
async fn init_tiles(texture_creator: &TextureCreator<WindowContext>) -> Result<Vec<Tile>, MyError> {
let mut tiles = create_tiles_from_json(&texture_creator, JSON_FILE_NAME).await?;
create_rotate_tiles(&mut tiles);
generating_adjacency_rules(&mut tiles);
Ok(tiles)
}
pub async fn create_tiles_from_json<'a>(
texture_creator: &'a TextureCreator<WindowContext>,
file_name: &str,
) -> Result<Vec<Tile<'a>>, MyError> {
let tile_list_data = load_json_data(file_name).await?;
let mut tiles = Vec::new();
for tile_data in tile_list_data.tile_list {
tiles.push(Tile::load(
texture_creator,
tile_data.src,
tile_data.edges,
tile_data.is_rotate,
)?);
}
Ok(tiles)
}
isRotateのフラグが立ったものに関しては回転バージョンのTileインスタンスを生成します。
90度、180度、270度の回転の3種類を追加するので、1/2π * n が行えるようにfor文は1始まりとします。
fn create_rotate_tiles(tiles: &mut Vec<Tile>) {
let mut new_tiles = Vec::new();
for tile in tiles.iter() {
if tile.is_rotate {
for j in 1..4 {
new_tiles.push(tile.rotate(j));
}
}
}
tiles.extend(new_tiles);
}
こちらの処理を終え、全てのTileインスタンスの生成は行えました。
各タイルの隣接性を作成
generating_adjacency_rules関数にて、全タイルの隣接関係の評価を行いそのタイルは 上、右、下、左にどのタイルとコネクト可能かを調べます。
fn generating_adjacency_rules(tiles: &mut [Tile]) {
let tile_edges: Vec<_> = tiles.iter().map(|tile| tile.edges.clone()).collect();
for (index, tile) in tiles.iter_mut().enumerate() {
tile.analyze(&tile_edges, index);
}
}
自分自身のedgesの0番目は上なので、他のタイルとは、下部にあたるedgesの2番目と接続となるので、edges[0]とedges[2]を評価します。
pub fn analyze(&mut self, tile_edges: &[Vec<String>], current_index: usize) {
for (index, edges) in tile_edges.iter().enumerate() {
if index == current_index {
continue;
}
// UP
if compare_edge(&edges[2], &self.edges[0]) {
self.up.push(index);
}
// RIGHT
if compare_edge(&edges[3], &self.edges[1]) {
self.right.push(index);
}
// DOWN
if compare_edge(&edges[0], &self.edges[2]) {
self.down.push(index);
}
// LEFT
if compare_edge(&edges[1], &self.edges[3]) {
self.left.push(index);
}
}
}
その際、edgesに格納されたままだと評価できないので、文字列を逆にする処理を入れています。
pub fn reverse_string(s: &str) -> String {
s.chars().rev().collect()
}
pub fn compare_edge(a: &str, b: &str) -> bool {
a == reverse_string(b)
}
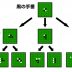
例えば、以下の様なタイルチップがあった場合、
※1 このタイルが保持するedgesは[”AAB”, ”BBB”, ”BAA”, ”ACA”]となります。
※2 絵から、同じタイルの上部と下部でコネクトできそうなのがわかります。
※3 実際に上部と下部は「AAB」と「AAB」
※4 しかしながら下部で保持しているedgesは「BAA」となるので片方文字列を反転し評価する必要があります。
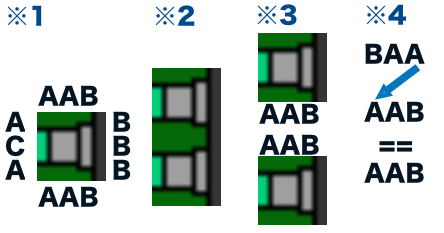
左右の評価も同様となります。
Grid 作成
最初に記述した、「グリッド内にセルとして全ての可能性として保持」のフローとなります。
まず、Grid全体の大きさを決めたいので定数DIM(dimension)を定義し、こちらでグリッド全体の大きさを決定します。
DIM * DIM(縦 * 横)で、Grid作成と同時に Cellを作成します。
pub const DIM: usize = 15;
from_valueファクトリーメソッドで、Cellのインスタンスを生成します。
fn init_grid(length: usize) -> Vec<Cell> {
(0..DIM * DIM)
.map(|_index| Cell::from_value(length))
.collect()
}
CellのsocketsはTileのindexとなります。つまり、初期状態は「全ての可能性を持った」状態となり、エントロピーも最大のTileの全体数となります。
pub struct Cell {
pub collapsed: bool,
pub sockets: Vec<usize>,
}
impl Cell {
pub fn from_value(value: usize) -> Cell {
Cell {
collapsed: false,
sockets: (0..value).collect(),
}
}
pub fn from_list(value: Vec<usize>) -> Cell {
Cell {
collapsed: false,
sockets: value,
}
}
}
(3分21秒経過)
Wave Function Collapse – 波動関数崩壊アルゴリズム メインフロー
準備は整いましたので、ここからWave Function Collapse – 波動関数崩壊アルゴリズム のメインフローとなります。
fn main_loop(grid: &mut Vec<Cell>, tiles: &[Tile]) {
let mut low_entropy_grid = pick_cell_with_least_entropy(grid);
if low_entropy_grid.is_empty() {
return;
}
if !random_selection_of_sockets(&mut low_entropy_grid) {
*grid = init_grid(tiles.len());
return;
}
wave_collapse(grid, tiles);
}
再度流れを振り返ると、
- エントロピーの低いセルを優先するため、グループ化して取得
- pick_cell_with_least_entropy
- タイルをランダムに選択、セルを1つの選択肢に確定
- random_selection_of_sockets
- 隣接するセルのソケットを評価し、各セルのエントロピーを減少
- wave_collapse
となります。
pick_cell_with_least_entropy関数
「エントロピーの低いセルを優先するため、グループ化して取得」を行っていきます。
まず、現在のgridの状態をシャローコピーしたいので、grid_copy変数に格納します。
そのcell自身がcollapsed、つまりセルが確定しているのであれば無視し、セルが確定していないものでフィルタリングします。
その後、セルのsocketsの数が少ない順、つまりエントロピーの低い順にソートを行います。
通常であればきちんと計算や重みつけなども考慮しますが、今回は単純に低エントロピーはsocketsの少ない順とします。
pub fn pick_cell_with_least_entropy(grid: &mut Vec<Cell>) -> Vec<&mut Cell> {
let mut grid_copy: Vec<&mut Cell> = Vec::new();
for cell in grid.iter_mut() {
if !cell.collapsed {
grid_copy.push(cell);
}
}
if grid_copy.is_empty() {
return Vec::new();
}
grid_copy.sort_by_key(|cell| cell.sockets.len());
let len = grid_copy[0].sockets.len();
let stop_index = grid_copy
.iter()
.position(|cell| cell.sockets.len() > len)
.unwrap_or(grid_copy.len());
grid_copy.truncate(stop_index);
grid_copy
}
その後、最小エントロピーのグループ化として、最初のcellのsocketsの数を調べそれを超える場合は排除します。
つまり、[1,2],[1,2],[1,2],[1,2,3] となった時点でそのindexを取得しtruncateでカットを行います。
random_selection_of_sockets関数
「タイルをランダムに選択、セルを1つの選択肢に確定」を行っていきます。
ここでは、見つからない場合の考慮も行います。
「見つからない場合」とは、制約ルールによってはコネクトできずパターンがなくなる事も発生することがあります。その際、再度最初からやり直すため Gridを初期化します。
if !random_selection_of_sockets(&mut low_entropy_grid) {
*grid = init_grid(tiles.len());
return;
}
random_selection_of_sockets関数は、最小エントロピーのグループからcellをランダムに選択し、collapsedをtrueにして確定フラグを立てます。そのcellのsocketsからどのタイルにするかもランダム選択し、表示するタイルを確定させます。
pub fn random_selection_of_sockets(grid_target: &mut Vec<&mut Cell>) -> bool {
let mut rng = rand::thread_rng();
if let Some(cell) = grid_target.choose_mut(&mut rng) {
(*cell).collapsed = true;
if cell.sockets.is_empty() {
return false;
}
if let Some(&pick) = cell.sockets.choose(&mut rng) {
cell.sockets = vec![pick];
true
} else {
false
}
} else {
false
}
}
(4分9秒経過)
wave_collapse関数
いよいよ、WFCのコアの部分に迫ってきました。
最後のフロー「隣接するセルのソケットを評価し、各セルのエントロピーを減少」となります。
改めて、ここで行っている事は、グリッド全体の左端から上下左右のセルのsockets、すなわちコネクトできるタイルのindexを見て、自分自身のcellの状態を変化させることです。
各セルの状態は、配置可能なtileを絞られることになるのですが、それがエントロピーの減少となります。
wave_collapseには、gridとtilesを引数に渡します。
wave_collapse(grid, tiles);
それでは、中身をみていきましょう。
pub fn wave_collapse(grid: &mut Vec<Cell>, tiles: &[Tile]) {
let mut next_grid: Vec<Option<Cell>> = vec![None; DIM * DIM];
for j in 0..DIM {
for i in 0..DIM {
let index = i + j * DIM;
if grid[index].collapsed {
next_grid[index] = Some(grid[index].clone());
} else {
let mut sockets: Vec<usize> = (0..tiles.len()).collect();
// Look up
if j > 0 {
cell_collapse(&mut grid[i + (j - 1) * DIM], "down", &mut sockets, tiles);
}
// Look right
if i < DIM - 1 {
cell_collapse(&mut grid[i + 1 + j * DIM], "left", &mut sockets, tiles);
}
// Look down
if j < DIM - 1 {
cell_collapse(&mut grid[i + (j + 1) * DIM], "up", &mut sockets, tiles);
}
// Look left
if i > 0 {
cell_collapse(&mut grid[i - 1 + j * DIM], "right", &mut sockets, tiles);
}
next_grid[index] = Some(Cell::from_list(sockets));
}
}
}
grid.clear();
grid.extend(next_grid.into_iter().filter_map(|cell| cell));
}
まず、次のGridの状態に書き換え用の空のベクターnext_gridをグリッド範囲分の幅で用意。
let mut next_grid: Vec<Option<Cell>> = vec![None; DIM * DIM];
チェックするセルの順番ですが、グリッドの左端から確認していくこととなります。
for j in 0..DIM {
for i in 0..DIM {
もし、対象のセルが確定していればそのセルはそのまま次のグリッドの状態に渡します。
if grid[index].collapsed {
next_grid[index] = Some(grid[index].clone());
}
配置できるsockets(エントロピー)を、まずは全可能性を持った状態で初期化を行います。tilesの数だけindexを持ったベクターを作成し、そこから絞っていきます。
let mut sockets: Vec<usize> = (0..tiles.len()).collect();
続いて、今のセルの上、右、下、左の順番で隣合うセルをチェックしていきます。
if j > 0 {
cell_collapse(&mut grid[i + (j - 1) * DIM], "down", &mut sockets, tiles);
}
jは行となり、j= 0は一番上の行となるので、最初の行に関してはこちらはスキップされます。まず一番最初に行われるセルは左上端のセルとなり、隣り合う右のセルをチェックすることになります。

cell_collapse関数で実際にcellの折りたたみを行うこととなります。
右のセルをチェックする場合、grid[i + 1 + j * DIM]で右側のcellを参照します。
自分自身に対して右側なので、そのセルは左側にコネクト可能なタイルを検証することになります。
cell_collapse(&mut grid[i + 1 + j * DIM], "left", &mut sockets, tiles);
...
fn cell_collapse(cell: &Cell, direction: &str, sockets: &mut Vec<usize>, tiles: &[Tile]) {
let valid_sockets = get_valid_sockets(cell, direction, tiles);
check_valid(sockets, &valid_sockets);
}
cell_collapse関数で行っていることは、get_valid_socketsでコネクトsockets(コネクト可能なタイルインデックス)を取得し、check_validで比較し存在しなければ引数で渡されたsocketsのindexは削除。となります。
get_valid_sockets関数
fn get_valid_sockets(cell: &Cell, direction: &str, tiles: &[Tile]) -> Vec<usize> {
let mut valid_sockets = Vec::new();
for &socket in &cell.sockets {
let valid = &tiles[socket].valid(direction);
valid_sockets.extend(valid);
}
valid_sockets
}
cellはチェック対象(流れ的に 最初は右側)のセルとなり、そのセルの持つsockets(タイルインデックス)分、tileのvalidメソッドで確認していきます。
右側のセルの場合は “left”となり、tileインスタンス生成時設定したleft、つまり左側にコネクト可能な tileのindexの配列を返却します。
pub fn valid(&self, direction: &str) -> Vec<usize> {
match direction {
"up" => self.up.clone(),
"right" => self.right.clone(),
"down" => self.down.clone(),
"left" => self.left.clone(),
_ => Vec::new(),
}
}
チェック対象のcellのsockets(tile)の数だけ、コネクト可能な tileのindexを追加します。
valid_sockets.extend(valid);
最後に、check_validで先程作成したコネクト可能なtileのindex全てが追加されたvalid_socketsと、チェック時に作成したsocketsを比較し、存在しなければ削除します。
fn check_valid(sockets: &mut Vec<usize>, valid_sockets: &[usize]) {
sockets.retain(|socket| valid_sockets.contains(socket));
}
ここで、エントロピーの減少が発生したことになります。
上下左右チェックし、一つでも置けない可能性があるのであれば崩壊することとなります。
※ 一方が「2, 4」しかコネクトの可能性がない例
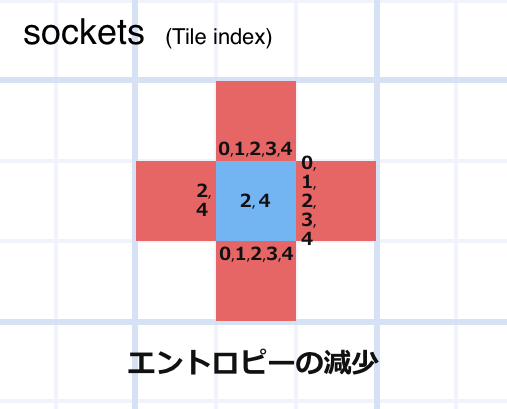
この様に、自分の上下左右のセルをチェックし、そのセルの影響で自分自身のエントロピーが減少し、伝播していくことが波動関数の崩壊となります。
グリッド全てのセルのチェックが終わると、grid自体を崩壊後のグリッドに置き換えます。
grid.clear(); grid.extend(next_grid.into_iter().filter_map(|cell| cell));
この様に、wave_collapse関数では隣り合うセルの状態を確認し、セルの持つsocketsの可能性を絞って行くことでエントロピー減少させて、再び低エントロピーからランダムに選択しタイルを確定。また、wave_collapse関数で隣り合うセルのチェック….。
と繰り返すことで、崩壊は伝播していきます。
描画
最後に描画処理となります。
fn draw(canvas: &mut Canvas<Window>, grid: &[Cell], tiles: &[Tile]) {
let w = GAME_WIDTH / DIM as u32;
let h = GAME_HEIGHT / DIM as u32;
for j in 0..DIM {
for i in 0..DIM {
let index = i + j * DIM;
let cell = &grid[index];
if cell.collapsed {
let tile_index = cell.sockets[0];
let tile = &tiles[tile_index];
tile.render(
canvas,
(i as u32 * w).try_into().unwrap(),
(j as u32 * h).try_into().unwrap(),
w,
h,
);
}
}
}
}
loopで、draw関数実行し、(fps挟んでないのでCPUを占有しちゃうかも) cell.collapsedの状態を監視し描画するかどうかを振り分けています。
それでは実行してみましょう。
はい。
いい感じにできましたね。
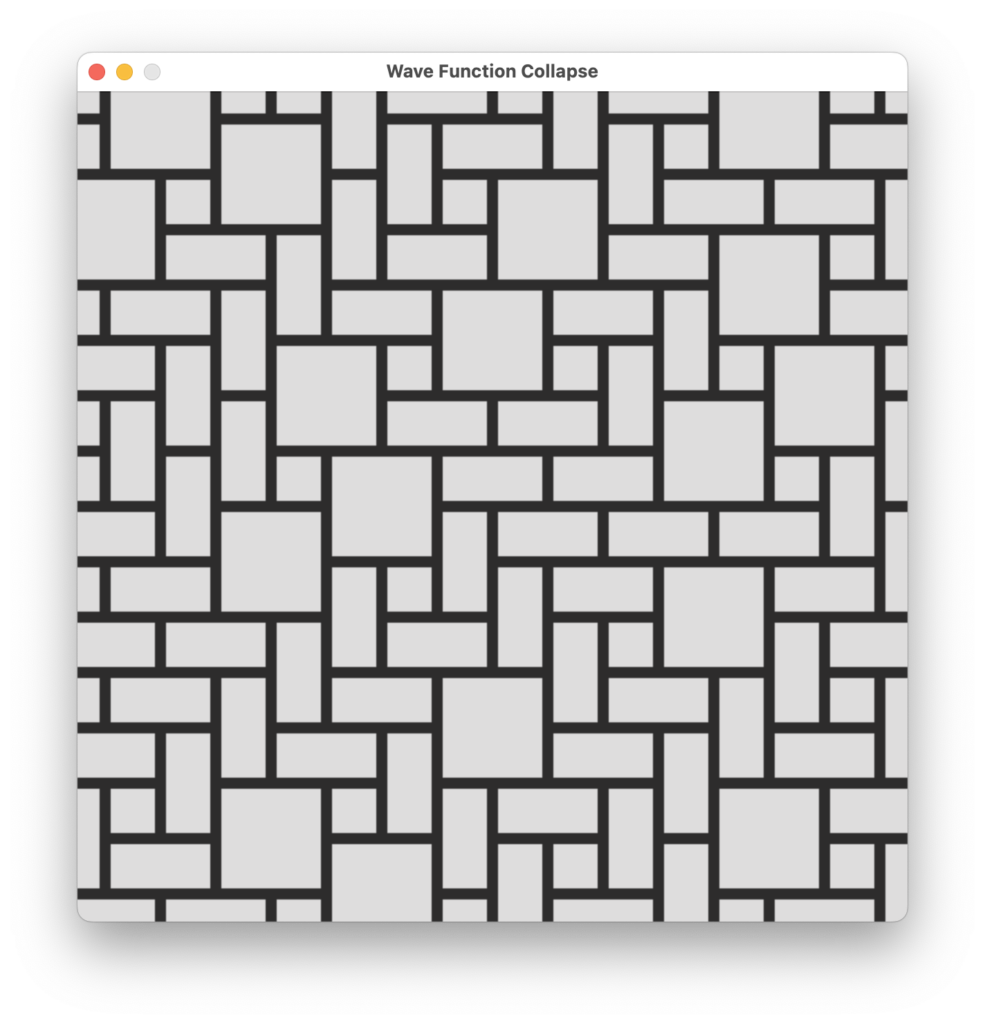
その他のサンプルも試してみましょう。

おお。いい感じですね。

いい感じだがちょっと調整必要。

こちらは部屋の図面ぽいですね。
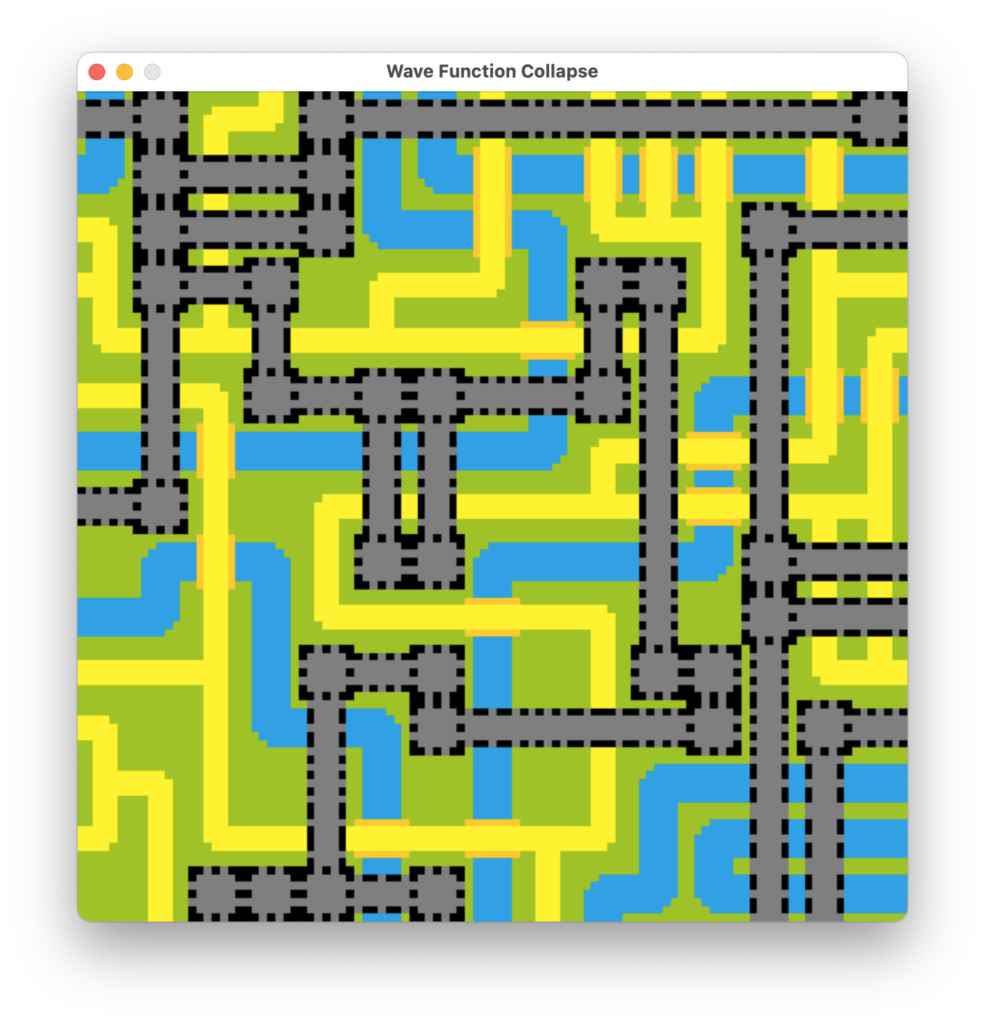
いい感じですが、ちょっと調整が必要そうですね。

これは、あっているのか。違いますよね。
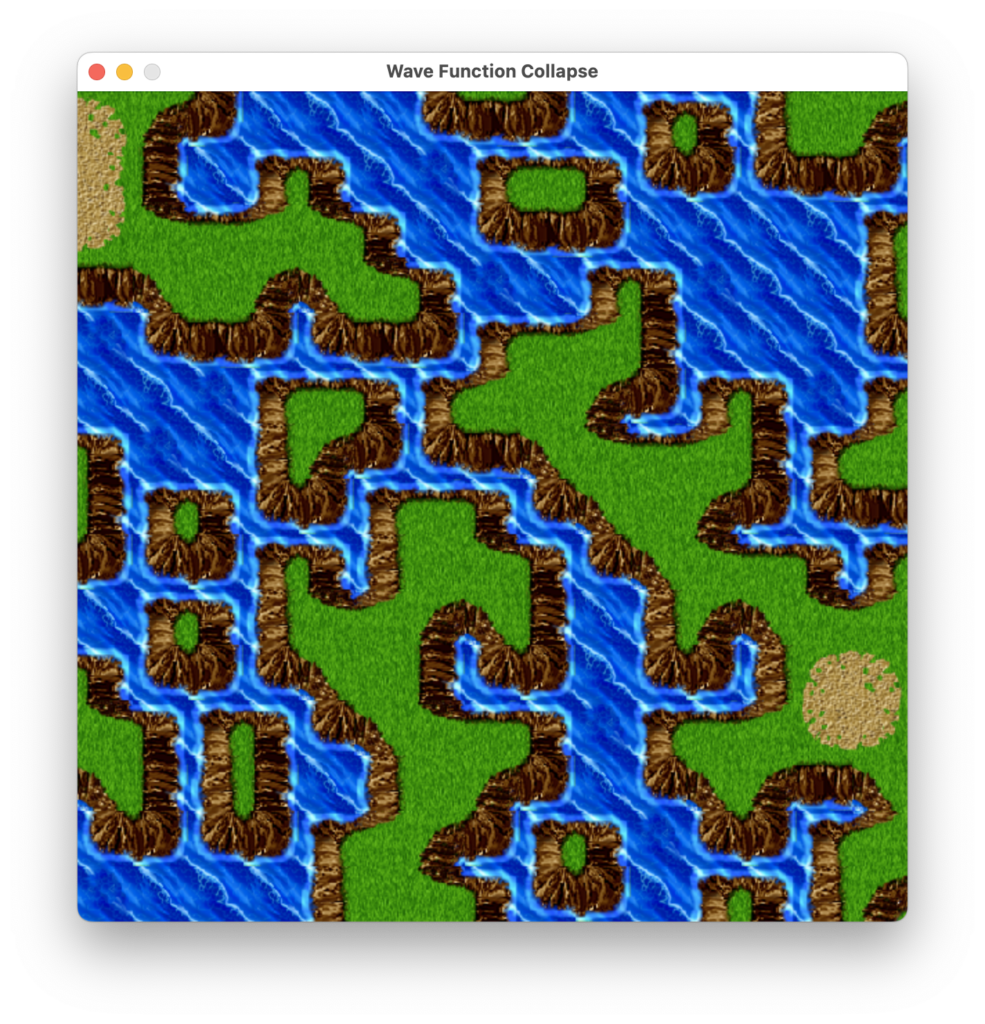
RPGマップも良い感じではありますが、調整が必要そう。
と、意図した通りに表示したのと、ちょっと違かったのと、制約の調整が必要そうなものもありましたが、取り敢えずは完成。制約の付け方で表示も異ってくるのも確認できました。
今回作成したソースはこちらになります。
https://github.com/webcyou-org/wave-function-collapse-rust/tree/main
それはそうと、実は、Flutter、Flameを用いても実装していましたが、やっぱRust実装のほうが起動、実行ともにパフォーマンスよく快適でした。しかしながら、Flutterの方が意図的な表示なっていたりして、Rust側の見直しが必要そう。
https://github.com/flame-games/wave-function-collapse
(5分12秒経過)
最後に
という訳で、今回はWave Function Collapse – 波動関数崩壊アルゴリズムのTile Modelを実装してみました。5分を大幅に過ぎてしまうんじゃないかと思っていましたが、5分12秒となんとか5分台に収められて良かったです。
参考文献
https://github.com/mxgmn/WaveFunctionCollapse
Doodle Insights #19: Logic Data Generation (feat. WFC made easy)