JavaScriptで、DOMを放り投げる処理
2024.07.27
この記事は最終更新日から1年以上が経過しています。
どもです。
今回は、JavaScriptで、DOM(HTML)を放り投げる処理についてです。
先にお見せすると、この様な処理になります。

特段難しい処理などではないのですが、ある日メンバーに実装をお願いしたところ「できない。」と返ってきたので、え。なんでと思った次第ではありました。
過去にもこの処理について、大分昔に書いた覚えがありますが、「できない」と言われたのが結構ずっとひっかかっていて今回改めて記事化してみました。
自分が仕事で「できない」と言ってこなかったのもあるか(「技術的には可能です」)、そういってしまうとエンジニアの価値を自分で下げていることと同じだぞ。と思いましたが、老害と思われたくないので(笑)それは告げず。「じゃぁいいよ」と言ってしまった。
そもそも、お願いした処理としては、上記の円形の移動よりももっと簡易なもので、タブを持ち上げる処理なので、上下の移動しかないです。
※ ツマミを持ち上げると全体が持ち上がる形。つまむのと放り上げで移動。
クリックでの上下の移動は実装できたみたいなのですが、掴んで投げるがどうやら難しかったみたいです。
処理実装
それでは実装していきたいと思いますが、まず考え方として、
質量は存在しないものとします。なので大きさによって運動量の変化もしない形とするので、運動の法則よりより簡易なものとなります。
しかしながら摩擦力などがないとDOM(円形)が止まらないので、空気抵抗が存在するものとします。
また、重力も存在しないものとします。なので、開始位置、終了位置、時間、距離が算出できれば簡潔するような簡易な内容となっております。
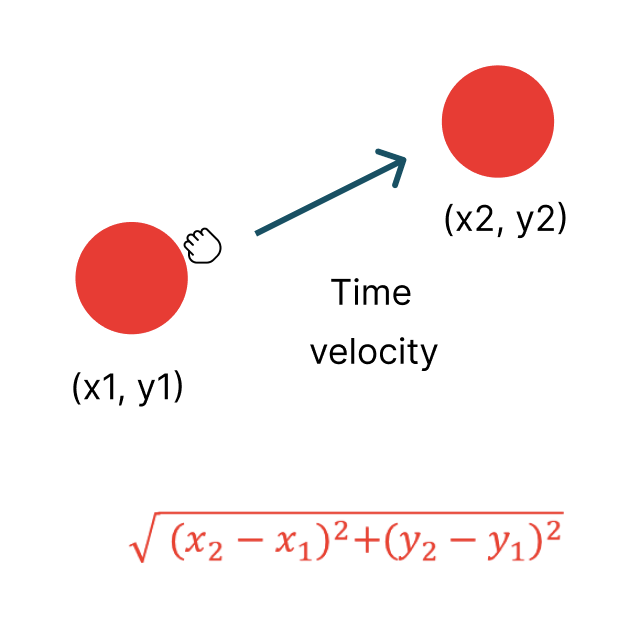
何はともあれ、操作に扱う円形を生成します。(CSSは省略)
<body>
<div id="circle"></div>
<script> const circle = document.getElementById('circle'); </script>
</body>
それぞれの変数と空気抵抗の係数(任意の値)を用意します。
let isDragging = false; let startX, startY, startLeft, startTop, startTime; let endX, endY, endTime; let velocityX, velocityY; const airResistance = 0.01;
まずは、円形を掴む処理。円形のDOMに対してマウスダウンイベントをアタッチします。
circle.addEventListener('mousedown', (e) => {
isDragging = true;
startX = e.clientX;
startY = e.clientY;
startLeft = circle.offsetLeft;
startTop = circle.offsetTop;
startTime = Date.now();
document.addEventListener('mousemove', onMouseMove);
document.addEventListener('mouseup', onMouseUp);
});
続いて、ドラッグ(円形移動)の処理。
function onMouseMove(e) {
if (isDragging) {
const currentX = e.clientX;
const currentY = e.clientY;
circle.style.left = `${startLeft + currentX - startX}px`;
circle.style.top = `${startTop + currentY - startY}px`;
}
}
円形のどの位置を掴んでもそのまま移動できるように処理。
続いてマウスアップの処理
function onMouseUp(e) {
if (isDragging) {
isDragging = false;
endX = e.clientX;
endY = e.clientY;
endTime = Date.now();
const elapsedTime = (endTime - startTime) / 1000;
velocityX = (endX - startX) / elapsedTime;
velocityY = (endY - startY) / elapsedTime;
document.removeEventListener('mousemove', onMouseMove);
document.removeEventListener('mouseup', onMouseUp);
applyPhysics();
}
}
elapsedTimeは経過時間となり、/ 1000を行い秒に変換。
x, yと各それぞれマウスアップされた位置を最初にクリックした位置で引き、経過時間で割って速度を求めます。
最後に、applyPhysicsで円形の移動を行います。
function applyPhysics() {
const move = () => {
const currentLeft = parseFloat(circle.style.left);
const currentTop = parseFloat(circle.style.top);
if (Math.abs(velocityX) > 0.1 || Math.abs(velocityY) > 0.1) {
velocityX *= (1 - airResistance);
velocityY *= (1 - airResistance);
circle.style.left = `${currentLeft + velocityX * 0.01}px`;
circle.style.top = `${currentTop + velocityY * 0.01}px`;
requestAnimationFrame(move);
}
};
move();
}
x, yと各それぞれ速度を加算し、移動させています。空気抵抗である、airResistanceで速度を減速し、加速度がなくなるまでrequestAnimationFrameでmoveの再帰処理を行います。
と、言うことで出来上がり。
しかしながら現状だと、直線上の移動などは良いが、複雑な動きや長時間掴んで動かすとすぐに変な方向へと行く。
これは、最初に円形を掴んだ(クリック)した場所を元にしてしまっているので、その時点からの時間や経路は円形を離した後(マウスアップ)の円形の運動には直接関係はなく、円形を離す前(マウスアップ)の数秒前の経路が影響するからです。
そこで、数ステップサンプリングし、そこから円形のベクトルを算出したいと思います。
まず、経路のポイントを何個確保するかの定数sampleSizeと、そのデータを保持するpositionsを定義。
let positions = []; const sampleSize = 5;
マウスダウンイベントでpositionsを初期化します。
positions = [];
続いてマウスダウンイベントの処理を変更
function onMouseMove(e) {
if (isDragging) {
const x = e.clientX;
const y = e.clientY;
positions.push({ x, y, time: Date.now() });
// 位置データを一定間隔で取得
if (positions.length > sampleSize) {
positions.shift();
}
circle.style.left = `${startLeft + x - startX}px`;
circle.style.top = `${startTop + y - startY}px`;
}
}
経路のポイントを何個確保するかを定義した定数sampleSizeの数だけサンプリング。
マウスアップイベントでpositionsの最後と最初を取得し、x, yのdelta、velocityを算出。
function onMouseUp(e) {
if (isDragging) {
isDragging = false;
const endTime = Date.now();
const elapsedTime = (endTime - startTime) / 1000;
if (positions.length > 1) {
const lastPos = positions[positions.length - 1];
const firstPos = positions[0];
const deltaX = lastPos.x - firstPos.x;
const deltaY = lastPos.y - firstPos.y;
velocityX = deltaX / elapsedTime;
velocityY = deltaY / elapsedTime;
}
document.removeEventListener('mousemove', onMouseMove);
document.removeEventListener('mouseup', onMouseUp);
applyPhysics();
}
}
applyPhysicsメソッドは前回と同様。
としたところで、記事最初のアニメの様な形となります。
これで完璧か。というとそうでもなく湾曲のマウスの経路を取ると、ちょっと意図した形にはならなかったりもするので、もっと作り込むのであれば、遠心力も考慮した計算なども含めてば良いでしょう。
次回、そちも考慮できた実装を紹介できればと思っております。
ではではぁ。
またまたぁ。